A Machine That Can Add
On the 4th year of college I ran into one of the most beautiful things I had ever seen: the adder.
I remember having a hard time containing the enthusiasm: you'd think that computing sums was something reserved for higher order intelligence, so it was mesmerizing seeing it in action by a machine.
In a base-2 adder (i.e. one that operates over binary numbers), you can enumerate all of the possible sums for single digit numbers. For example:
| a | b | a + b |
|---|---|---|
| 0 | 0 | 00 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 10 |
This table represents all of the values that a + b take for all possible combinations of a and b (e.g. when 0 + 0 = 0 and 0 + 1 = 1). Notably, 1 + 1 = 10 (1 + 1 = 2 in decimal), which needs two bits to be represented. We'll call that extra bit the carry. For example:
| a | b | carry | sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
It is easy to verify that the following logical expression leads to the same results of addition:
- sum = a xor b
- carry = a and b
With the following truth table:
| a | b | c = a && b | s = a xor b |
|---|---|---|---|
| F | F | F | F |
| F | T | F | T |
| T | F | F | T |
| T | T | T | F |
Interestingly, a circuit can be built using logical gates that can perform these logical operations:
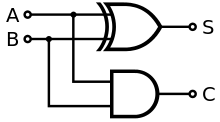
That gives you the ability to add two single-digit numbers: given a and b it computes sum and carry.
To add numbers with two digits, we take the carry c0 value that was computed in the first digit and combine that with the second digits a1 and b1:
| a1 | b1 | c0 | a1 + b1 | c1 | s1 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 00 | 0 | 0 |
| 0 | 0 | 1 | 01 | 0 | 1 |
| 0 | 1 | 0 | 01 | 0 | 1 |
| 0 | 1 | 1 | 10 | 1 | 0 |
| 1 | 0 | 0 | 01 | 0 | 1 |
| 1 | 0 | 1 | 10 | 1 | 0 |
| 1 | 1 | 0 | 10 | 1 | 0 |
| 1 | 1 | 1 | 11 | 1 | 1 |
Which, can be built as the following digital circuit, which is known as the full adder:

The full adder is pretty awesome, because if you keep chaining the carry bits with the next digits to be added, you can sum arbitrarily long binary numbers:

This is a circuit that is capable of computing the sum of two binary numbers.
A machine that can add.